Project 3a

OBJECTIVE

To forecast our firm’s demand for a product in order to plan future operations and also planning the course of action in various possible scenarios. Develop a DSS and implement it.

Overall Model to be developed: FD = TID x RD/N

TID - Total Industry demand for the overall industry is important to determine overall market growth.

TID variables

· Estimated Average Advertising (a measure of the average amount spent on advertising by the industry)

· Estimated Average Price (a measure of the average price charged for the product by the industry)

RD - Relative Demand for any quarter; RD= FD/AFD where FD is our firm’s demand and AFD is the average demand per firm in the industry

RD variables

· Prel – Relative price (P/ AvgP), where P is price charged by our firm and AvgP is the average price charged by the industry

· Arel - Relative Advertising amount (A/ AvgA), where A is advertising amount spent by our firm and AvgA is the average advertising amount spent by the firms in the industry

· RD1 – Relative demand for the previous quarter

MS - Market Share; MS= RD/N

Influence Diagram

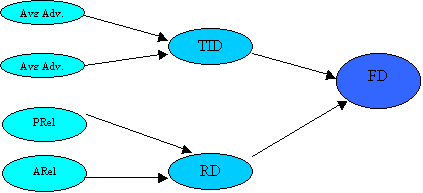
The Demand forecasting model

Model 1 for TID:

From our analysis in the previous project

Estimated TID=14218.07 + 645.98(Quarter)

¨ Regression analysis was performed using only Quarter as the independent variable

¨ The P value for the intercept is 0 and the P value for Quarter is .001, this shows that the variable “Quarter #” is Significant and there is a no chance of making a Type I error.

¨ R Squared is 48% indicates that 48% of the variance in TID has been explained

¨ This model is more useful for long term forecasting

Model 2 for TID

Estimated TID = 130249 +132 (Quarter) - 358 (Avg_Price) + 0.263(Avg_Adv)

¨ The P values were all very low except for the variable quarter (0.2187). This indicates that Quarter is an insignificant variable.

¨ The R Squared for the model is 90.7%, which means that 90.7% of the variance in the TID has been explained.

¨ The effect of the variable quarter is already explained by the other 2 variables

Therefore the new model without the “Quarter” variable is

¨ Estimated TID= 164336.17 - 445.17(Avg. Price) +0.26(Avg. Adv.)

¨ The R Squared for the model is 89.7%, which means that 89.7% of the variance in the TID has been explained. The value dropped slightly as we have one less variable.

¨ The P values were all very low. This shows that the model is very accurate and has a low probability of error

¨ This model is more useful in short term forecasting

Relative Demand (RD)

The estimated regression equation for the RD model is RD= 16.13 –16.44(PREL) +0.77(AREL) +0.53(RD1).

· The P values for all of the variables are extremely low, and hence all the variables are significant.

· R squared is 95.7% suggests 95.7% of the variance been explained.

Firm Demand (FD):

Using the above equations, we can arrive at FD

Estimated FD = TID x MS, since MS =RD/N where N is the number of firms in the industry

Estimated FD = (130249 +132 (Quarter) - 358 (Avg_Price) + 0.263(Avg_Adv)) x 1.612 – 1.644(PREL) + 0.077(AREL) +0.53(RD1)

· The implementation model is used to help forecast Firm Demand. The values in the model can be changed at the user’s discretion.

DSS for Estimating FD- Implementation

Explanation of the DSS model:

Inputs		Outputs
Quarter# "t"	20
		Total Industry Demand	30520.14
Estimates for Industry (for Qtr "t")
Estimated Average Price	366	Relative Demand	1.23
Estimated Average Advertising	105000
Number of Firms in Industry	10	Market Share	0.123
Our Decisions (for Qtr. "t")		Our Firm's Estimated Demand	3755.30
Price	359.00
Advertising	100000.00	Average Demand	3052.014
Historical Data for Qtr = t-1
Our firm's Demand	3000
Total Industry Demand	32850
Calculations
Relative Price (Qtr = t)	0.98
Relative Advertising (Qtr = t)	0.95
Average Demand (Qtr = t-1)	3285
Our Firm's Relative Demand (Qtr = t-1)	0.91

· These are our uncertain variables

· These are our potential decisions

· These inputs are from our historical database

· These are our outputs

Inputs for the model:

External Variables: (Factors controlled by environment)

· These factors can be determined by descriptive statistics or looking at estimated trends.

(Click here for assistance in choosing inputs)

Estimated Average Price

Estimated Average Advertising

Number of Firms in Industry

Variables that we can control: (Our decisions)

· These are determined through analysis

Our Price

Our Advertising

Historical Data (Previous Quarter’s data)

· We have this data available (Click here for the data)

Our firm's Demand

Total Industry Demand

Outputs:

· TID

· MS

· FD

(Click here for a functional DSS model)

Use of the model:

This model can be used to predict various market scenarios and how our firm can react to it. It helps us to determine optimum values for our decision variables.

Sensitivity Analysis :

· Helps us determine the effect of changing price and advertising inputs on the firm’s demand and market share

· Step 1: Attain a market share of at least 10.5% by changing only the price variable . The resulting price was found to be $359

· Step 2: Attain a market share of at least 10.5% by changing only the advertising expenditure. The resulting amount was found to be $140000

Sensitivity analysis
Using expected averages of price and advertising ( 363 & 110000),
firm's advertising kept constant
Price sensitivity
	INITIAL	Trial I	Trial II	Trial III	Trial IV
Price	365	364	361	360	359
Adv.	100000	100000	100000	100000	100000
MS	0.079033	0.083577	0.09721	0.101754	0.106298
Firm Demand	2200.997	2364.756	2880.309	3060.252	3244.241
Using expected averages of price and advertising ( 363 & 110000),
keeping price constant
Advertisement sensitivity
	INITIAL	Trial I	Trial II	Trial III	Trial IV
Price	365	365	365	365	365
Adv.	100000	105000	110000	115000	140000
MS	0.079033	0.082575	0.086116	0.089658	0.107
Firm Demand	2200.997	2406.974	2622.159	2846.552	4106.64

Goal Seek:

· To achieve a market share of 11.5% - using values of expected averages of price and advertising (363 & 110000)

· Step 1 : Keeping Advertising constant and see by how much the price has to be reduced in order to achieve our goal

· Step 2 : Keeping price constant and see by how much the advertisement spending has to be increased in order to achieve our goal

	Initial	* By changing price	** By changing Adv.
`		keeping Adv constant	keeping price constant
Inputs
Quarter# "t"	20	20	20
Estimates for Industry (for Qtr "t")
Estimated Average Price	363	363	363
Estimated Average Advertising	110000	110000	110000
Number of Firms in Industry	10	10	10
Your Decisions (for Qtr. "t")
Price	359	357.09	359
Advertising	100000	100000	112000
Historical Data for Qtr = t-1
Your Demand	3000	3000	3000
Total Industry Demand	32850	32850	32850
Outputs
Total Industry Demand	30520	31373	33640
Relative Demand	1.06	1.15	1.15
Market Share	10.63%	11.50%	11.5%
Your Firm's Estimated Demand	3244	3608	3862

However it may be unrealistic to drop prices to $357 or increase the advertising budget to112000. We need to get better understanding of our cost and profitability to determine this

Scenario analysis

From sensitivity analysis, we determined Price to be $359 and advertising amount spent to be 100000 to achieve a MS of at least 10.5%. Keeping these values constant, we will look at various scenarios

· Scenario1 (Most Likely): Estimated average price is $363 and Estimated average advertising is 110000. Our MS is 10.6%

· Scenario2 (Worst Case): Estimated average price is $360 and Estimated average advertising is 115000. Our MS is 9%

· Scenario 3 (Best Case): Estimated average price is $366 and Estimated average advertising is 105000. Our MS increases 12.3%

Scenario Summary
Scenario	One	Two	Three
Changing Cells:	Most Likely	Worst Case	Best Case
Estimated Average Price	363	360	366
Estimated Average Advertising	110000	115000	105000
Result Cells:				Average
Our Firm's Estimated Demand	3244.24	2735.33	3755.30	3244.96
Market Share	0.106	0.090	0.123	0.106